[ad_1]
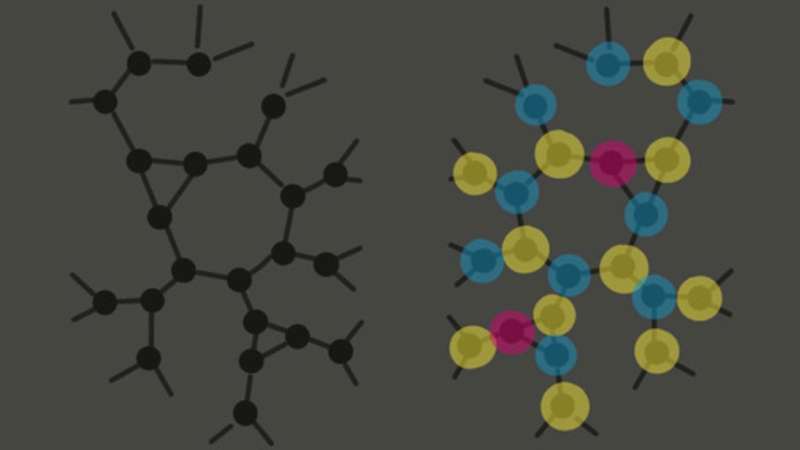
알고리즘이 이 두 그래프를 구분할 수 있습니까? 왼쪽의 균일한 그래프는 오른쪽의 심은 용액과 구별하기 어렵습니다. 출처: Jess Banks, 2021 학습 이론 컨퍼런스 요약 발표
컴퓨터 과학에서 그래프 색칠 문제는 고전입니다. 지도 색칠 문제에서 영감을 받아 다음과 같이 묻습니다. 링크로 연결된 노드 네트워크가 주어지면 링크가 동일한 색상의 두 개를 연결하지 않도록 각 노드를 색칠하는 데 필요한 최소 색상 수는 얼마입니까? 적은 수의 색상과 링크의 경우 솔루션을 찾는 것은 간단합니다. 가능한 모든 조합을 시도하십시오. 그러나 링크가 증가함에 따라 문제는 더욱 제한적입니다. 링크가 너무 많고 색상이 충분하지 않으면 솔루션이 전혀 존재하지 않을 수 있습니다.
레지던트인 폴리매스 크리스 무어(Cris Moore)는 “그러면 아마도 해결책이 있을 수 있지만 찾기가 매우 어려운 매력적인 중간 영역이 있으며, 아마도 없을 수도 있지만 없다는 것을 증명하기가 어려운 또 다른 영역이 있습니다.”라고 말합니다. SFI 교수. 이는 기존의 문제 해결 알고리즘이 이를 찾을 수 없다는 것을 의미한다고 그는 말합니다. 예를 들어 무작위 색상으로 시작하여 노드 색상을 뒤집기 시작하면 이러한 숨겨진 솔루션 중 하나를 찾지 못할 것입니다.
2021년 학습 이론 컨퍼런스에서 발표된 새로운 논문에서 Moore와 그의 동료들은 이러한 숨겨진 솔루션으로 문제를 구성하는 새로운 방법을 설명합니다. 이 그룹에는 전 SFI 학부생이자 현재 박사 과정을 밟고 있는 학사 후 인턴인 수학자 Jess Banks가 포함되어 있습니다. 캘리포니아 버클리 대학교에서.
그들은 일종의 수학적 악마의 옹호자 역할을 하여 문제에 접근합니다. 그들은 문제를 해결하는 대신 그 안에 숨겨진 솔루션을 사용하여 새롭고 복잡한 문제를 만듭니다. 무어는 “우리는 해결사인 솔루션 파인더의 흰색 모자를 벗고 거의 암호화와 같은 까다로운 문제를 설계하는 사람의 검은색 모자를 씁니다.”라고 말합니다. “해결책이 숨겨져 있습니다.”
연구원들은 솔루션을 숨기는 미묘한 방법을 고안했다고 Moore는 말합니다. 그리고 그들이 이러한 문제를 문제 해결 알고리즘에 넘길 때 알고리즘은 비어 있게 됩니다. “많은 알고리즘이 해결할 수 없는 문제를 만들 수 있거나 문제가 있는지 말할 수 있다면 해결책“라고 Moore는 말합니다. “그러면 이러한 문제가 어려운 영역을 찾았다는 강력한 증거가 있습니다.”
이 논문에는 여러 종류의 알고리즘이 이렇게 생성된 문제에 대한 솔루션을 찾지 못한다는 것을 증명하는 정리가 포함되어 있습니다. 이는 연구자들이 해결책을 찾기 어려운 이 “단단한” 영역의 상전이 경계를 식별하는 데 그 어느 때보다 가까워졌음을 의미합니다. 또는 해결책이 없음을 증명합니다.
Moore는 문제를 정확하게 식별하기 위한 지속적인 노력은 시스템이 더 제한적일 때 시스템이 어떻게 변하는지 묻는 물리학의 추측에서 비롯되었다고 말합니다.
“우리의 모험은 물리학의 이러한 추측과 계산을 수학적 증명으로 바꾸는 것이었습니다.” 그리고 이 분야를 계속 발전시키는 유일한 방법은 수학, 물리학, 컴퓨터 과학의 도구가 서로 겹치는 강점을 활용하는 것이라고 그는 말합니다.
Afonso S. Bandeira et al, 스펙트럼 심기 및 무작위 그래프의 절단, 착색성 및 커뮤니티 반박의 경도. arXiv:2008.12237v1 [cs.CC], arxiv.org/abs/2008.12237
에 의해 제공
산타페 연구소
소환: 연구원들은 어려운 문제의 미개척 영역을 조사하기 위해 https://phys.org/news/2021-10-probe-unexplored-space-hard-problems에서 2022년 1월 24일에 검색한 악마의 옹호자(2021, 10월 12일)를 재생합니다. HTML
이 문서는 저작권의 보호를 받습니다. 사적 연구 또는 연구를 목적으로 하는 공정한 거래를 제외하고는 서면 허가 없이 어떤 부분도 복제할 수 없습니다. 콘텐츠는 정보 제공의 목적으로만 제공됩니다.
원본 보기
[ad_2]

![[PHYS ORG] 어려운 문제의 미개척 공간을 조사하기 위해 연구원들은 악마의 옹호자 역할을 합니다.](https://color.re.kr/wp-content/uploads/2022/01/to-probe-an-unexplored-1280x640.jpg)
![[PHYS ORG] 다윈의 새새끼들 중 일부가 노란색 부리를 가지고 있는 이유](https://color.re.kr/wp-content/uploads/2022/01/why-some-of-darwins-fi-440x264.jpg)
![[PHYS ORG] 온도가 높아지면 와인 포도의 맛이 더 좋아지는데, 그 기간은 얼마나 될까요?](https://color.re.kr/wp-content/uploads/2022/01/increasing-temperature-440x264.jpg)
![[PHYS ORG] 색맹 물고기는 시력이 어떻게 진화했는지 보여줍니다.](https://color.re.kr/wp-content/uploads/2022/01/colorblind-fish-show-e-440x264.jpg)
![[DEZEEN] 밝은 색상의 스케이트 공원](https://color.re.kr/wp-content/uploads/2022/01/yinka-ilori-skatepark-hero-1024x576-440x264.jpg)